Topic outline
-
¡Hola desde el final del curso ahora!Lean esto por favor.Les pedimos que completen la encuesta que está acá: https://forms.gle/yusv8ioXoQcg833G7Es muy importante que CADA UNO pueda darse un ratio para responder las preguntas, lleva 5/10 minutos y nos sirve muchísimo para poder saber cómo vivieron ustedes el curso, cosas para cambiar y cosas para reafirmar.
La encuesta es anónima así que siéntanse libres de responder con total honestidad, nos es muy importante que así sea.
---------------------------------------------------------------------------Hola. Les damos la bienvenida al curso de Matemática Discreta, en su edición 2023. Los docentes a cargo somos Mariana Haim (coordinadora) y Santiago Robaina (ayudante).Las clases serán teórico-prácticas, en el horario de 8:30 a 11:30 los martes, y de 8:30 a 10:00 los jueves. Salón 206 los martes, salón 102 los jueves.Este espacio será utilizado como apoyo al curso, que se desarrolla en forma presencial. De todas maneras, pueden entrar aquí los estudiantes que necesiten realizar el curso de manera virtual: eventual virtualidadEl formato de trabajo será en una modalidad que incluirá mucho trabajo grupal de tipo "taller", por lo que la asistencia presencial es fuertemente incentivada.Esta página será una herramienta esencial para la comunicación quienes participemos del curso, estudiantes y docentes.En esta página encontrarán:- Información general del curso: programa, bibliografía, prácticos, método de aprobación.
- Avance del curso y resultados de las pruebas.
- Un foro de anuncios de suscripción obligatoria donde se irá anunciando todo lo importante sobre el curso.
- Un foro de consultas donde ustedes pueden escribir y al que Santiago y Mariana estaremos atentos. Los incentivamos a usarlo, y también a responder, comentar, cuando tienen algo que aportar. En ese foro podemos escribir todos.
Objetivos del curso:
Además del valor en sí mismo de los temas que se darán en el curso, se pretende aprovechar el hecho de que los temas son elementales (en el sentido de autocontenidos y de fácil enunciado-no por ello de fácil resolución) para:
- familiarizar al estudiante con nociones y notaciones básicas en matemática;
- presentar al estudiante problemas de enunciado elemental, que lo motiven a construir por sí solo teoremas generales que puedan resolverlos. De esta manera, el estudiante entenderá la necesidad de una definición, de una notación, de un lema, de un enunciado formal, de una demostración;
- familiarizar al estudiante con el trabajo grupal y constructivo, como modelo de lo que hace luego un matemático profesional: trabaja en colaboración, y construyendo teoría a partir de los problemas que se plantea. Siguiendo esta línea de trabajo, no distinguiremos clases teóricas de prácticas.
-
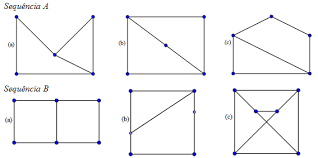
Jueves 25 (se cambió por Viernes 26): muestra de parciales y primeras miradas sobre grafos.
Martes 29: Generalidades sobre grafos. Lema de handshaking. Isomorfismos, encajes, subgrafos. Grafo completo y complemento de un grafo. Grafo bipartito. Caminos en grafos. Si existe un camino de v a w, entonces existe uno simple. Conexión. Trabajamos sobre el Repartido 7, que tiene que estar terminado para el jueves.
Jueves 1: Trabajo sobre el Repartido 7. Subgrafo inducido por un conjunto de vértices. Teorema de existencia de circuitos eulerianos en multigrafos conexos. (Seguimos un poco con esto en la próxima clase).
Martes 6: Teorema de existencia de recorridos Eulerianos. Ciclos y caminos hamiltonianos. Criterio de Ore. Trabajo sobre el Repartido 8.
Jueves 7: Trabajo sobre Repartidos 7 y 8
Martes 13: Representación planar de un grafo: definición y ejemplos. Regiones, grado de una región y lema de handshaking para regiones. Característica de Euler de un grafo conexo. Prueba de que
y 
no son planares. Empezaron a trabajar con el ejercicio 3 del Repartido 9. Enunciado (vago) del Teorema de Kuratowski. Explicaremos los detalles en la clase del jueves.Jueves 15: Repartido 9
Martes 20: Mapas políticos y grafos planares asociados. Definición de
-coloración. Teorema de los 6 colores. Teorema de los 5 colores.Jueves 22: Trabajo sobre el Repartido 9
Lunes 26: Parcial 3 (el martes 27 hay paro por los 50 años del Golpe de Estado)