Biofísica 2023: Ej 2 examen 19/02/2019

Me mareo un poco la parte de calcular por q factor se modifica el complejo. Al disminuir la enzima yo supongo que debe disminuir tambien.

Re: Ej 2 examen 19/02/2019

de Acosta Servetto Ismael - domingo, 28 de enero de 2024, 18:06

Hola María,

Cuidado con las unidades en tus cálculos. Las concentraciones de

$C, E, S$ no están en las mismas unidades.

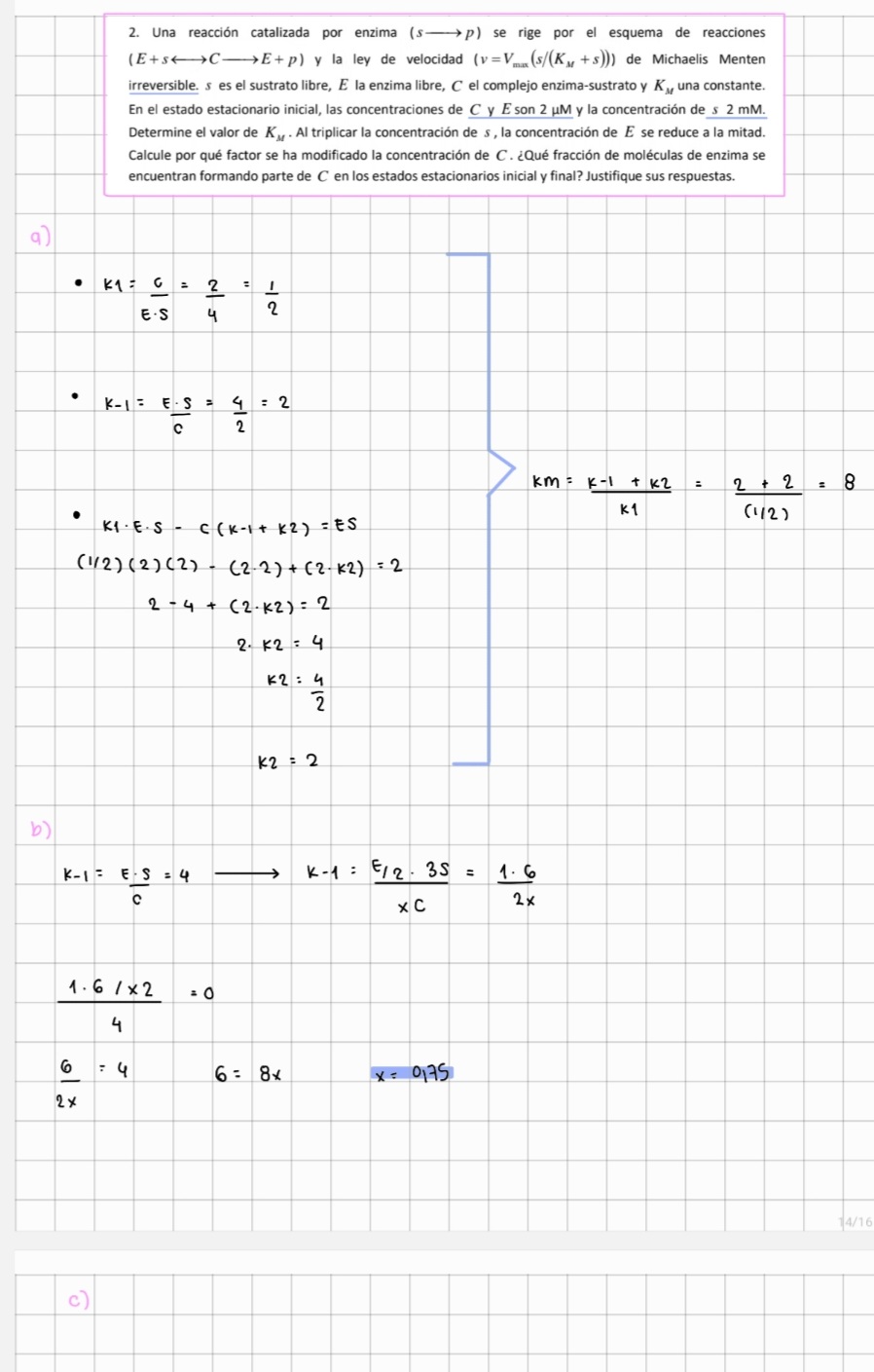
Las constantes resultan en:

$k_1 = \frac{C}{ES} = \frac{2 \times 10^{-6} M}{(2 \times 10^{-6} M)(2 \times 10^{-3} M)} = 500 M^{-1}$

$k_{-1} = \frac{ES}{C} = 1/k_1 = 2 \times 10^{-3} M$

En el estado estacionario tenemos que:

$dC/dt = k_1 ES - C k_{-1} - C k_2 = 0$

Despejando para

$k_2$ se tiene que:

$k_2 = \frac{k_1 ES - k_{-1}C}{C} \simeq 0,998$

Por lo que la constante

$K_M$ viene dada por:

$K_M = \frac{k_{-1}+k_2}{k_1} = 2 \times 10^{-3} M$

Para la nueva situación tenemos que:

$E^* = E/2 = 1 \times 10^{-6} M = 1 \mu M$

$S^* = 3S = 6 \times 10^{-3} M = 6 mM$

El factor por el que se modifica la concentración de complejo es:

$C^*/C = \frac{k_1E^*S^*}{k_1 ES} = \frac{\frac{E}{2}3S}{ES} = \frac{3}{2} = 1,5$

$C^* = 1,5C = 1,5(2 \times 10^{-6} M) = 3 \times 10^{-6} M = 3 \mu M$

La fracción de moléculas que forman complejo en los estados estacionarios inicial y final es:

$(\frac{C}{C+E})_{inicial} = 0,5$

$(\frac{C^*}{E^*+C^*})_{final} = 0,75$

Notar que a pesar de haber disminuido la concentración de enzima libre a la mitad, al triplicar la de sustrato tenemos una mayor fracción de moléculas de enzima formando complejo.

Saludos,