Física no lineal - 2025: Bifurcaciones: primer pantallazo

Intoducción

Los sistemas que vimos hasta ahora en una dimensión eran relativamente sencillos y con pocas chances de representar sistemas físicos realistas. Sin embargo presentan algunos aspectos remarcables. El primero de ellos es el cambio cualitativo de las soluciones cuando se cambian los parámetros.Los parámetros son magnitudes que se cambian lentamente por medio de un agente externo.

Los cambios cualitativos que mencionamos se denominan bifurcaciones, concepto fundamental en los sistemas nolineales. Comenzaremos con la bifurcación de nodo-silla que de alguna forma es la más famosa.

1. Bifurcación nodo-silla

Esta bifurcación representa el mecanismo básico de creación y destrucción de puntos fijos.

Consideremos un sistema dado por

$\dot{x}= r + x^2$

donde $r$ es un parámetro de control que da cuenta de una variación del sistema inducida por un mecanismo externo. Esta variación se supone que está dada y es mucho más lenta que las escalas propias del sistema. Cuando $r$ es fácil ver que hay 2 puntos fijos uno estable y el otro inestable. A medida que $r$ tiende a $0$ por la izquierda los puntos fijos se van acercando hasta que en el caso límite de $r=0$ colapsan en un punto fijo que es semi-estable (es decir, estable frente a perturbaciones en una dirección e inestable en la otra). Para $r>0$ ya no quedan puntos fijos. Decimos que en $r=0$ ocurrió una bifurcación de nodo-silla. Como decíamos antes el sistema cambia cualitativamente en dicho valor de $r$ .

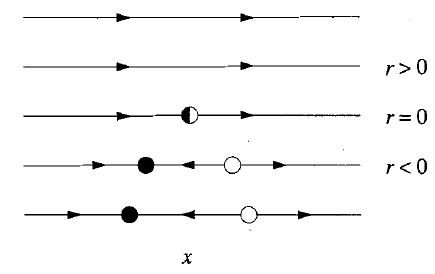
Gráficamente se puede ver de la siguiente forma

Una representación muy útil de las bifurcaciones se obtiene por medio de los diagramas de bifurcaciones donde se representan las soluciones de equilibrio (en este caso los puntos fijos)

usualmente las soluciones estables se grafican punteadas y las estables continuas.

Otra representación es:

bif nodo silla

Formas normales:

Todas las bifurcaciones tienen asociada una forma genérica de expresarlas denominada forma normal. En el caso de la nodo-silla dado un sistema

$\dot{x}= f(x,r),$

la forma normal se escribe como

$\dot{x}= a (r - r_c) + b (x- x^*)^2+ ...$

donde

$a = \frac {\partial f}{\partial r}|_{x^*,r_c}$ y $b = \frac 12 \frac {\partial^2 f}{\partial x^2}|_{x^*,r_c}$

Esta bifurcación es de alguna forma la más corriente de todas.

El tema formas normales es muy amplio, se puede encontrar más información en Guckenheimer y Holmes (1983).

2. Bifurcación transcrítica

En muchas sistemas se da que un punto fijo existe para todos los valores de un parámetro, por ejemplo en la ecuación logística la solución nula existe siempre por más que en ciertas situaciones es inestable. La bifurcación transcrítica es el mecanismo estándar de intercambio de estabilidad.

Partimos de una ecuación del tipo

$\dot{x}= r x - x^2 ,$

se puede ver que la solución $x=0$ siempre existe, además para $r$ tenemos otro punto fijo (inestable) negativo, mientras que para $r>0$ tenemos además de $x=0$ un punto fijo (estable) positivo.

El diagrama de bifurcaciones resulta

3. Bifurcación de tridente (u horquilla)

En este caso consideramos un sistema físico que tenga una simetría, en esta caso una simetría izquierda derecha (si cambiamos $x$ por $-x$ el sistema no cambia).

Algo que aún no dijimos es que las bifurcaciones pueden clasificarse según el término de mayor orden en supercríticas o subcríticas.

En este caso empezamos con la supercrítica, La forma normal es del tipo

$\dot{x}= r x - x^3 ,$

se puede ver que la solución $x=0$ siempre existe. Para $r$ esta solución es estable. Por otro lado para $r>0$ la solución $x=0$ cambia su estabilidad y aparecen dos nuevos puntos fijos simétricos (ambos estables).

El diagrama de bifurcaciones resulta

Ejemplo

Consideramos el sistema $\dot{x}= - x + \beta \tanh x$ . Mostramos que este sistema tiene una bifurcación de horquilla supercrítica en $x^*=0$ y $\beta=1$ .