Dudas sobre momentos dipolares.
Buenos días tratando de hacer el ejercicio 1 me surgen varias dudas sobre como pensar el momento dipolar.
Voy a ir ejemplificando mis dudas con el ejercicio 1.
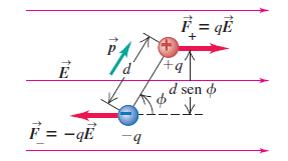
En este ejercicio se nos pide calcular la fuerza y el torque que se ejercen sobre un dipolo debido a un campo eléctrico externo.
Supongo que la posición de las partículas es arbitraria, en este caso me surge la duda de si siempre la fuerza neta va a ser igual a 0. (ver imagen que adjunto)
Por otro lado, repasando del curso de física 2 tenemos que  . Antes el calculo del torque era dipolar, pero ahora que dimos con mayor profundidad, ¿para el torque debemos considerar, el momento monopolar, dipolar y cuadripolar?.
. Antes el calculo del torque era dipolar, pero ahora que dimos con mayor profundidad, ¿para el torque debemos considerar, el momento monopolar, dipolar y cuadripolar?.
Por otro lado me surgen algunas dudas sobre los cálculos del momento cuadripolar, en la formula:
No me queda claro quien es  . En el caso del ejercicio 1
. En el caso del ejercicio 1
 supongo que
supongo que  seria la coordenada en x de la partícula 1,
seria la coordenada en x de la partícula 1, seria la coordenada y de la misma partícula, pero
seria la coordenada y de la misma partícula, pero  no tengo claro si es el vector respecto al origen o la distancia a este.
no tengo claro si es el vector respecto al origen o la distancia a este.
Desde ya muchas gracias.