Electromagnetismo 2021: Pr 6 ejercicio 3

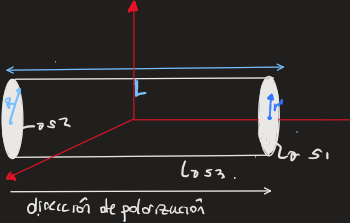
Hola buenos días, tratando de hacer el ejercicio 3 me surgen algunas dudas, comento como planteo el ejercicio.

Primero que nada respecto a la letra, cuando pide calcular el campo eléctrico que resulta de la polarización en un punto del eje del cilindro.¿Refiere a un punto interior o exterior del cilindro?.

Yo interprete que hay que dividirlo en dos casos pero no se si es correcto.

Que haciendo los calculos correspondientes primero con un punto exteriror, llego a que el campo es igual a 0, lo que si no estoy equivocado tiene sentido ya que debido a tener una polarización uniforme y como se demostró en clase la carga total encerrada es 0, por Gauss necesariamente el campo debe dar cero.

Re: Pr 6 ejercicio 3

de BORRA MANUEL - sábado, 23 de octubre de 2021, 14:28

Me imagino que interprete mal lo que dice el libro, pero menciona que el calculo dentro y fuera de un dielectrico es el mismo para un punto exterior o interior. Página 106 del Griffits.

Yo me tire a por estos calculos:

$\phi(r)=\frac{1}{4\pi\epsilon_0}\bigg(\oint_{S_0}\frac{\vec{P}\cdot\vec{n}da^\prime}{|\vec{r}-\vec{r}^\prime|}+\int_{V_0}\frac{-\nabla^\prime \vec{P}dv^\prime}{|\vec{r}-\vec{r}^\prime|}\bigg)$

Debido a que la polarización es uniforme se tiene que

$\nabla\vec{P}=0\rightarrow\int_{V_0}\frac{-\nabla^\prime \vec{P}dv^\prime}{|\vec{r}-\vec{r}^\prime|}=0$ .

Por lo que considerando que

$P$ es uniforme y que la simetría del problema nos permite utilizar coordenadas cilíndricas. Además de que la polarización es a lo largo del cilindro, tomando que dicha dirección es según

$\hat{i}$ , tenemos que

$\vec{P}\cdot\vec{n}da^\prime=Pda^\prime=Pr^\prime dr^\prime d\theta$ sobre la cara lateral del cilindro, ya que en las tapas el ángulo que forma el vector polarización y el normal es 0.

$\phi(r)=\frac{P}{4\pi\epsilon_0}\bigg(\int_{S_3}\frac{r^\prime dr^\prime d\theta}{|\vec{r}-\vec{r}^\prime|}\bigg)$ con

$S_3$ cara lateral.

Finalmente

$\phi(r)=\frac{PL(R^2-L^2)^{1/2}}{2\epsilon_0}\hat{k}$ siendo

$L$ el alrgo del cilindro Y a no ser que le pifie en las cuentas que seguramente sea eso, me daría que tanto dentro como fuera del cilindro el campo es 0

Que inicialmente era para un punto exterior pero por lo que comenta el libro vale para ambos casos.

Re: Pr 6 ejercicio 3

de De Polsi Gonzalo - miércoles, 27 de octubre de 2021, 10:12

Primero una precisión, sería la divergencia

$\nabla \cdot \vec{P}$ , no el gradiente

$\nabla \vec{P}$ .
En las tapas el ángulo que forman el vector polarización y la normal es 0 y por tanto el producto interno NO es cero... el producto interno de la normal y el vector polarización es, justamente, cero en la cara lateral que vos llamás

$S_3$ ... Además, tené cuidado como manejas esa integral (fijate en las notas de clase).

Saludos

Re: Pr 6 ejercicio 3

de De Polsi Gonzalo - miércoles, 27 de octubre de 2021, 10:02

Hola Manuel, qué tal?

En primer lugar te comento que este ejercicio lo discutimos en clase (ya ayer quedaron subidas las notas)... quizás encontrás allí lo que sea que precises.
Por otro lado, el razonamiento que hacés (respecto de usar Gauss) no es correcto. Recordá que Gauss es útil para hallar el campo eléctrico si la simetría te lo permite... que la carga encerrada sea cero sólo te indica que la integral

$\oint \vec{E} \cdot \hat{n} da = 0$ , pero esto no implica que

$\vec{E}$ sea cero.

La letra pide en un punto genérico del eje, por lo que son ambos casos efectivamente.

Saludos