Buenas tardes como están? les consulto acerca del ejercicio 4A del examen de febrero 2022.
Les cuento lo que plantee:
Me quedaron dos ecuaciones
1) d. sen α = n . λ1 (siendo λ1 760nM )
2) d. sen α = (n + 1/2) . λ2 (siendo λ2 nuestra incógnita)
Procedi a dividir ambas ecuaciones entre si, obteniendo:
1 = (2 . λ1) / (5/2 . λ2 )
Despejo la incógnita:
λ2= 4 . λ1 / 5
λ2=608 nM
Si bien me quedo dentro del espectro visible, no me da ni cerca del resultado marcado. No se cómo debería encararlo.
Gracias!
Rosina: te equivocas al dividir miembro a miembro las ecuaciones...
La cosa sería así:
La cosa sería así:
Máximo con el rojo (760 nm) en m=3: d.senθ= m.λ = 3×760 = 2280 nm
En esta posición se forma un mínimo: 2280 nm = (n+½) λ
Es decir que: λ= 2280 nm / (n+½)
Ahora le doy valores enteros a n desde 0 hasta obtener el menor valor dentro del rango visible.
Esto resulta para n= 5 y resulta λ= 415 nm
Se entiende? De lo contrario vuelve a consultar.
Héctor, gracias por tu explicación!
Lo que no me queda del todo claro es la parte de darle valores enteros a n. Tenia entendido que la letra ya me daba ese dato. ¿Por qué debo hacer eso hasta obtener el menor valor dentro del rango visible?
Lo que no me queda del todo claro es la parte de darle valores enteros a n. Tenia entendido que la letra ya me daba ese dato. ¿Por qué debo hacer eso hasta obtener el menor valor dentro del rango visible?
Rosina: Te daba el n correspondiente al máximo para el rojo, pero no para el otro color. es decir n estaba indeterminado. Entonces empiezo a variar el n y a obtener distintos valores λ hasta que este valor se hace menor que la menor longitud de onda del espectro visible.
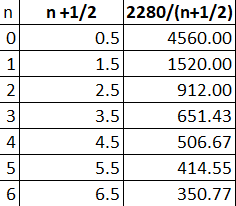
Se entiende ahora?
Gracias Héctor! Se entiende si.
Y eso es algo que debería hacer siempre?
Y eso es algo que debería hacer siempre?
Para este tipo de ejercicio en que el n no queda definido, sí.
