Hola, quería consultar si es correcto usar regla de tres para los ejercicos 10 y 11?
Hola Jimena,
Respuesta corta: no. Respuesta larga: estos problemas se enmarcan en el tema 'ley de escalas'. La regla de 3 supone una relación lineal entre las magnitudes; sin embargo las magnitudes aquí no dependen linealmente de los parámetros que cambian entre individuos.
Respuesta corta: no. Respuesta larga: estos problemas se enmarcan en el tema 'ley de escalas'. La regla de 3 supone una relación lineal entre las magnitudes; sin embargo las magnitudes aquí no dependen linealmente de los parámetros que cambian entre individuos.
Por ejemplo, pensemos en el ejercicio 10: ¿el peso de una persona es
proporcional a su altura?¿o lo es a su volumen? (asumiendo densidad
uniforme - digamos de agua). Entonces, un cambio en la altura, por
ejemplo pasar de 
, implica que el volumen pasa de 
. Y dependiendo de si la masa es proprocional a la altura o el volumen, cambia la respuesta. En este caso el modelo simple diría que la masa es proporcional al volumen.
, implica que el volumen pasa de . Y dependiendo de si la masa es proprocional a la altura o el volumen, cambia la respuesta. En este caso el modelo simple diría que la masa es proporcional al volumen.Pensalo en esta línea y cualquier cosa volvé a consultar si no se entiende,
Saludos,
Santiago
He leido en la resolución del práctico del año pasado que la respuesta para el ejercicio 10 sería: m = 66 kg, W = 6,5 × 10^2 N
Sin embargo, no sé que procedimiento se usó para llegar a dicho resultado. No logro llegar a este resultado con mis cálculos. Podría ayudarme a comprenderlo mejor? Gracias.
Sin embargo, no sé que procedimiento se usó para llegar a dicho resultado. No logro llegar a este resultado con mis cálculos. Podría ayudarme a comprenderlo mejor? Gracias.
Edito: creo que fue un error de cifras significativas de mi parte... podría compartirselo y decirme si lo estoy razonando correctamente?
Saludos y gracias!
No sé como subir esto, espero estar haciendolo correctamente 😅
Confirmeme si lo puede ver 😆
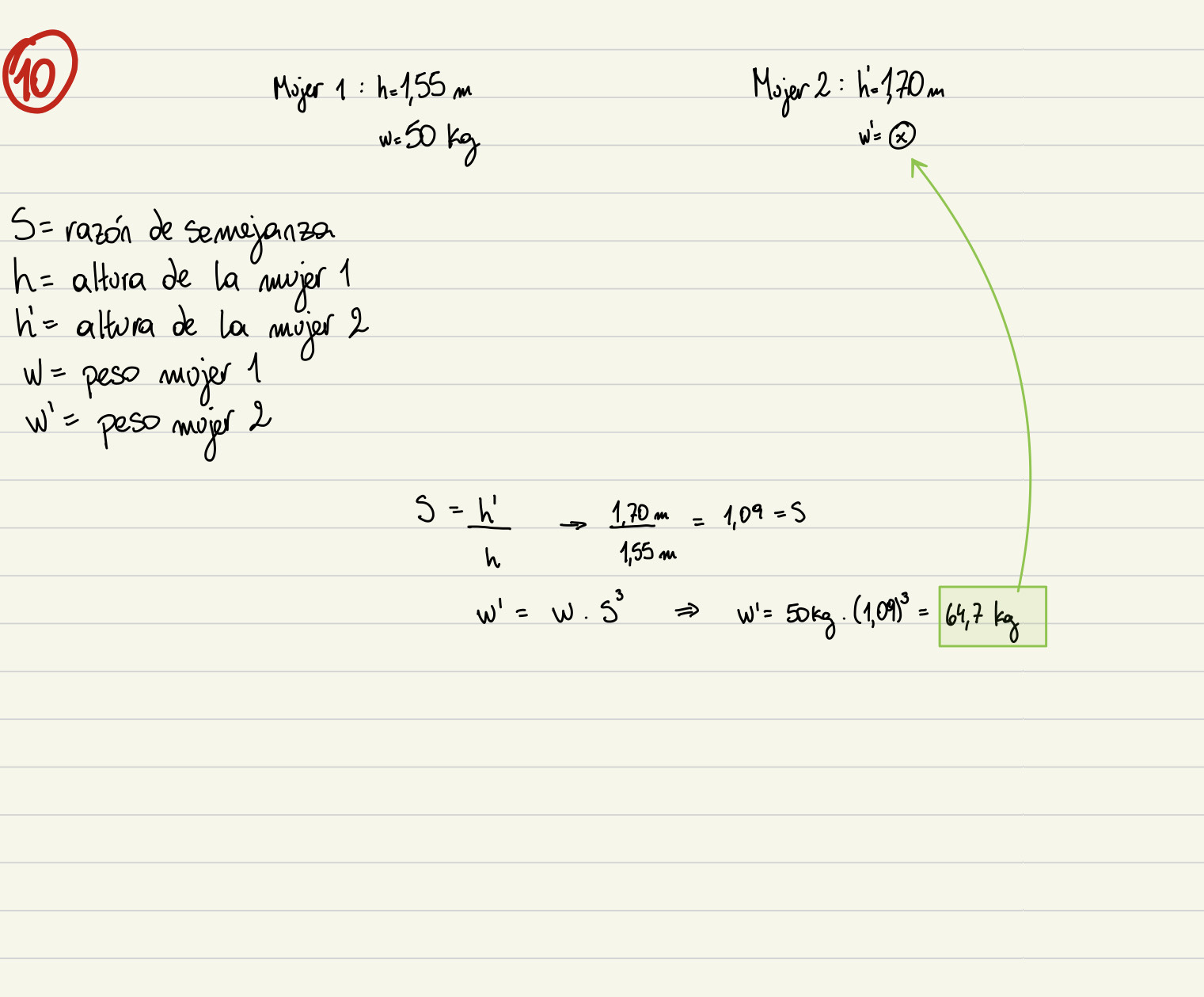
El razonamiento está perfecto, como sospechabas es nomás un tema de redondeo. Como comentaba recién en el foro, no está mal hacer cálculos intermedios, pero sugiero que si los hacen, trabajen con más de 3 cifras - al menos 4. En este caso, el cociente de las alturas con 4 cifras te queda 1.097, y ya con eso te queda los 66. Si lo redondeas a 3, tené cuidado que sería 1.10, lo cual quizás es demasiadas pocas cifras.
En resumen: muy bien resuelto, detalle de redondeo.
Saludos!
En resumen: muy bien resuelto, detalle de redondeo.
Saludos!
En este ejercicio hay que tener un poco de cuidado con una observación: el peso que una persona puede levantar es proporcional a la fuerza que es capaz de realizar. ¿de acuerdo con esto? Si soy capaz de realizar una fuerza de 100N, puedo levantar un objeto de 10kg del suelo (100N de peso). Si soy capaz de realizar una fuerza de 200N, puedo levantar un objeto de 20kg.
Pero la fuerza no es proporcional al volumen de la persona, sino a la sección transversal de sus músculos - es algo que discutirán quizas en más detalle en clase y sino está en el material teórico del curso. El área transversal depende de s^2. Por ende, deberías llegar a que la persona más alta puede levantar unas 1.61 veces el peso máximo que puede levantar la más baja.
Saludos!
Pero la fuerza no es proporcional al volumen de la persona, sino a la sección transversal de sus músculos - es algo que discutirán quizas en más detalle en clase y sino está en el material teórico del curso. El área transversal depende de s^2. Por ende, deberías llegar a que la persona más alta puede levantar unas 1.61 veces el peso máximo que puede levantar la más baja.
Saludos!
Buenas, estuve leyendo estos comentario respecto al ejercicio 11, pero no estoy pudiendo llegar a la cifra de 1.61, y no logro darme cuenta cuál es el cálculo que me está faltando realizar. Dejo en la foto el razonamiento que realicé.
Gracias, saludos
Hola Sofía,
Un comentario: k es la relación entre las dimensiones lineales de los objetos semejantes, en este caso el dato que tenemos es la altura. Entonces, directamente k=(h'/h). Y luego, el peso máximo que puede levantar una persona es proporcional a la fuerza máxima que puede realizar, la cual es a su vez, en los modelos simples vistos en clase, proporcional a la sección transversal de los músculos es decir que aumenta entre objetos semejantes como la relación k al cuadrado.
Un comentario: k es la relación entre las dimensiones lineales de los objetos semejantes, en este caso el dato que tenemos es la altura. Entonces, directamente k=(h'/h). Y luego, el peso máximo que puede levantar una persona es proporcional a la fuerza máxima que puede realizar, la cual es a su vez, en los modelos simples vistos en clase, proporcional a la sección transversal de los músculos es decir que aumenta entre objetos semejantes como la relación k al cuadrado.
Espero que esto aclare! Cualquier duda volvé a preguntar.
Saludos