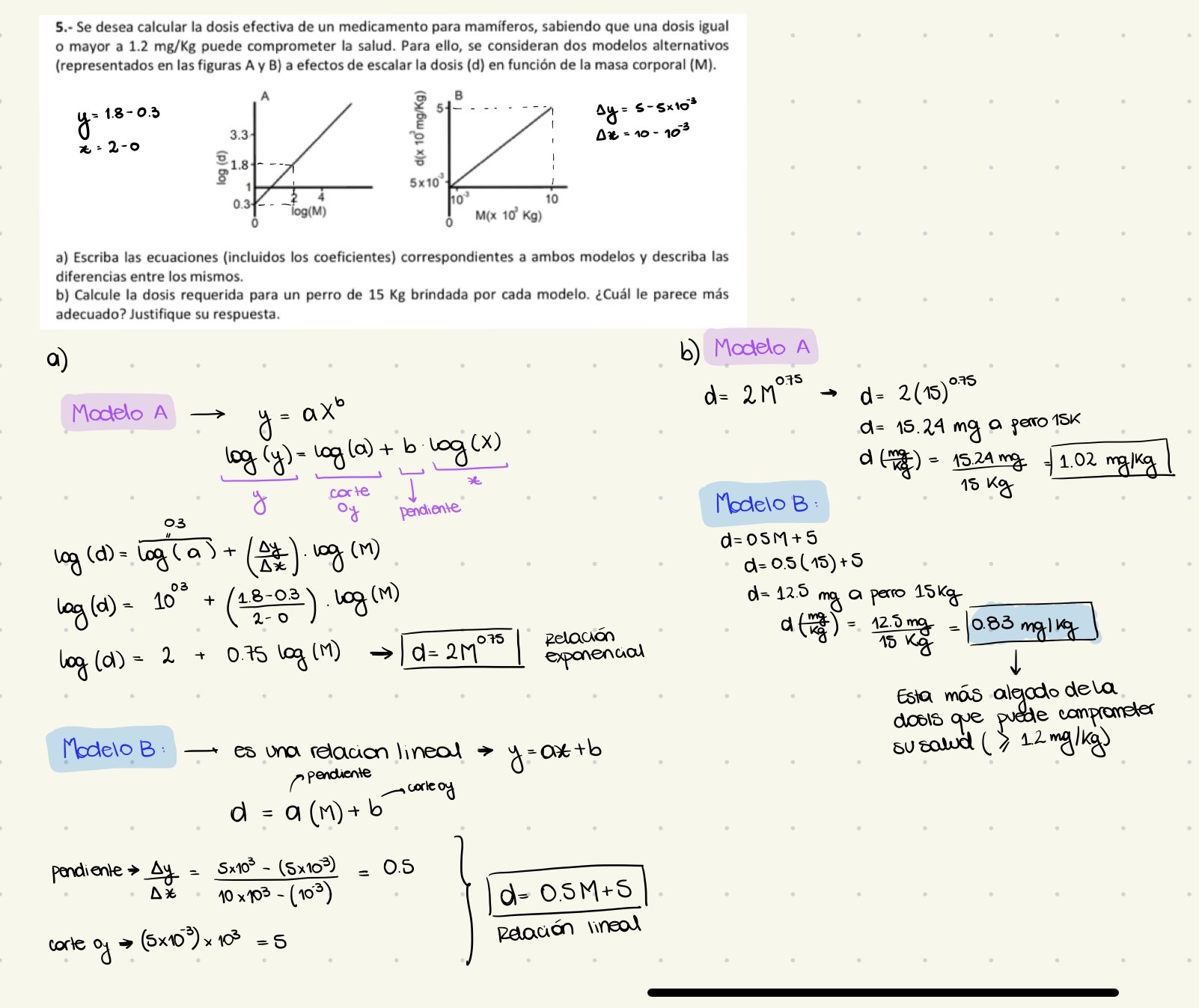
Biofísica 2023: Consulta de Examen 16/02/2022

Buen día, mando consulta del ejercicio 5 en el examen de Febrero 2022:

"Se desea calcular la dosis efectiva de un medicamento para mamíferos, sabiendo que una dosis igual o mayor a 1.2 mg/Kg puede comprometer la salud. Para ello, se consideran dos modelos alternativos (representados en las figuras A y B) a efectos de escalar la dosis (d) en función de la masa corporal (M).

a) Escriba las ecuaciones (incluidos los coeficientes) correspondientes a ambos modelos y describa las diferencias entre los mismos. b) Calcule la dosis requerida para un perro de 15 Kg brindada por cada modelo. ¿Cuál le parece más adecuado? Justifique su respuesta."

Mi pregunta es de la parte (b): ¿es correcto y suficiente el fundamento de que el modelo B es más adecuado para tratar un perro de 15 kg porque se encuentra mas alejado de la dosis que puede ser perjudicial para la salud? Me surge esta duda ya que según la resolución de la parte a y parte de la b, en realidad las dosis no son tan diferentes.

Dejo una foto de mi planteo del ejercicio.

Re: Consulta de Examen 16/02/2022

de Acosta Servetto Ismael - sábado, 27 de enero de 2024, 20:48

Hola Victoria,

Este ejercicio resultó ser un poco confuso en cuanto a la presentación de las gráficas, concretamente la gráfica del modelo B.

Efectivamente la ecuación para el Modelo A establece que:

$d = 2 M^{0.75}$

Dando una dosis total (en $mg$ ) de: $d = 15,25 mg$ la cual implica que por cada kilogramo de perro la dosis es de unos: $d_{a} = 1.016 \frac{mg}{kg} < d_{letal}$ .

Para la gráfica del modelo B como bien señalas, el modelo es lineal de la forma:

$d = aM +b$

Donde,
$a = 1/2$
$b = 0$

Es importante que notes lo siguiente: las unidades de la dosis en el modelo B están dadas en $mg/kg$ por lo que sustituyendo por la masa del perro ya obtenemos directamente la dosis por kilogramo.

Esto implica que: $d_{b} = 7,5 \frac{mg}{kg} > d_{letal}$

Por tanto el modelo A (que es alométrico) es mejor que el modelo lineal.

Saludos,