Ej 5 del examen

Ej 5 del examen

de SANTORO MARÍA -
Número de respuestas: 2

Hola, hoy en el examen pregunte como resolver el ejercicio 5 y me dijeron que había uno similar en el práctico, quería saber si se referían al ejercicio 1 o a cual por favor. En el ejercicio 1 te pide los pesos sinápticos que hagan que N3 se comporte de una forma determinada, entonces ahí hice una tabal de la verdad con esos datos (condición de N3 solo activa si N1 y N2 inactivas) y luego usando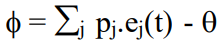

halle los pesos y el umbral. 

Pero en el caso del examen me daba los pesos sinápticos y umbrales pero yo no sabia ni las entradas ni las salidas, entonces no entiendo como hacerlo, tenia que probar con e= 0 o e=1 en todos los casos del circuito? 

Muchas gracias.

En respuesta a SANTORO MARÍA

Re: Ej 5 del examen

de Acosta Servetto Ismael -
Hola María,

La idea del ejercicio del examen era probar todas las combinaciones de entradas de  E_1, E_2, E_3 y evaluar con sus respectivos pesos las combinaciones para  N_1, N_2, N_3, N_s utilizando las dos ecuaciones vistas en el práctico de Redes Neuronales. 

e(t+1) = H(\Phi) = \left\{ \begin{array}{ll} 0 & si & \Phi < 0 \\ \\ 1 & si & \Phi \ge 0 \end{array} \right.

\Phi (t) = \sum_{i=1} ^{n} p_i e_i - \theta

Si no conté mal hay 8 combinaciones posibles de valores de entrada para la terna: 

(E_1, E_2, E_3) =\left( \begin{matrix} 1 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{matrix} \right)

Si hice bien las cuentas (chequéalas), de todas las combinaciones posibles, solo hay una salida (esto es  N_s = 1 ) cuando  E_1 o  E_2 están prendidas (ese "o" es exclusivo, es decir, una o la otra) y al mismo tiempo E_3 está apagada. 

En la parte (b) se pedía armar un circuito de una sola neurona procesadora que al computar las 8 combinaciones ejecutara la misma función que el circuito anterior. Si intentas calcular los pesos y el umbral que debería tener esa hipotética neurona encontrarás que el sistema de inecuaciones es incompatible, por lo que no es posible simplificar el circuito a una sola neurona de tres entradas. 

Espero haberme hecho entender con el razonamiento, 
Saludos,