Diagrama de temas
-
Para suscribirse a la lista de difusión, entrar acá: http://listas.cmat.edu.uy/listinfo/seminario_educacion_22
Martes 23/08: Santi y Mariana (eje: primera parte del capítulo "Lamentation")
Jueves 1/09: Juan y Marcos (eje: segunda parte del capítulo "Lamentation")
Jueves 8/9: Sara Vilar del Valle
Jueves 15/9: Luciana y Micaela (eje: artículo de Thurston)
Jueves 22/9: Matías y Rodrigo (eje: artículo de Thurston)
Jueves 29/9: Antonio Cafure
Jueves 6/10: paro
Jueves 13/10: Ariel Affonso
Jueves 20/10: Anthony y Mathias (eje: blog de Tao)
Jueves 27/10: Cecilia Calvo
Jueves 3/11: Mariana y Santiago (eje a definir)
Jueves 10/11: Gonzalo Frasca
Jueves 17/11: cierre con propuesta a definir
-
A cargo de Mariana y Santiago.
Lectura eje: primera mitad del capítulo Lamentation del libro de Lockhart (enseñanza de la matemática y de la enseñanza en general)
1) Hicimos el ejercicio de preguntar "Qué es la matemática" en diversos contextos, destacamos los siguientes tipos de respuesta:
- la madre de todas las ciencias; todo; sin matemática no hay nada; sirve para todo
- el estudio de objetos abstractos y sus relaciones, y su aplicación a la realidad
- lo que sirve para contar, medir, las cuentas, los números
- tipos de respuesta que la ligan con la asignatura liceal y la forma de enseñarla, cosas como "lo peor que me pasó en la vida"
2) Hicimos el ejercicio de preguntarnos qué es la música. Vimos la necesidad de nosotros mismos de dar una definición, de dar una respuesta acabada, y lo absurdo de ello. Pensar en qué es "enseñar música" es una buena forma de pensar en qué es "enseñar matemática", como propone Lockhart.
3) ¿Es realmente posible enseñar?
Dejamos planteada la siguiente dicotomía: experiencias matemáticas/contenidos matemáticos
El sistema educativo (en matemática y en otras áreas, pero en matemática se hace más evidente) está más concentrado en la parte de los contenidos (resultados, notaciones, algoritmos) que en la de las experiencias (ideas, hallazgos, errores, conjeturas).
Propusimos empezar a mirar las cosas que suceden en el aula (sea el aula que sea) con el lente de esta dicotomía.
Un ejemplo que pone Lockhart en este sentido es:
Experiencia matemática: comparar las áreas del rectángulo y del triángulo (con base el lado de abajo del rectángulo) del siguiente dibujo
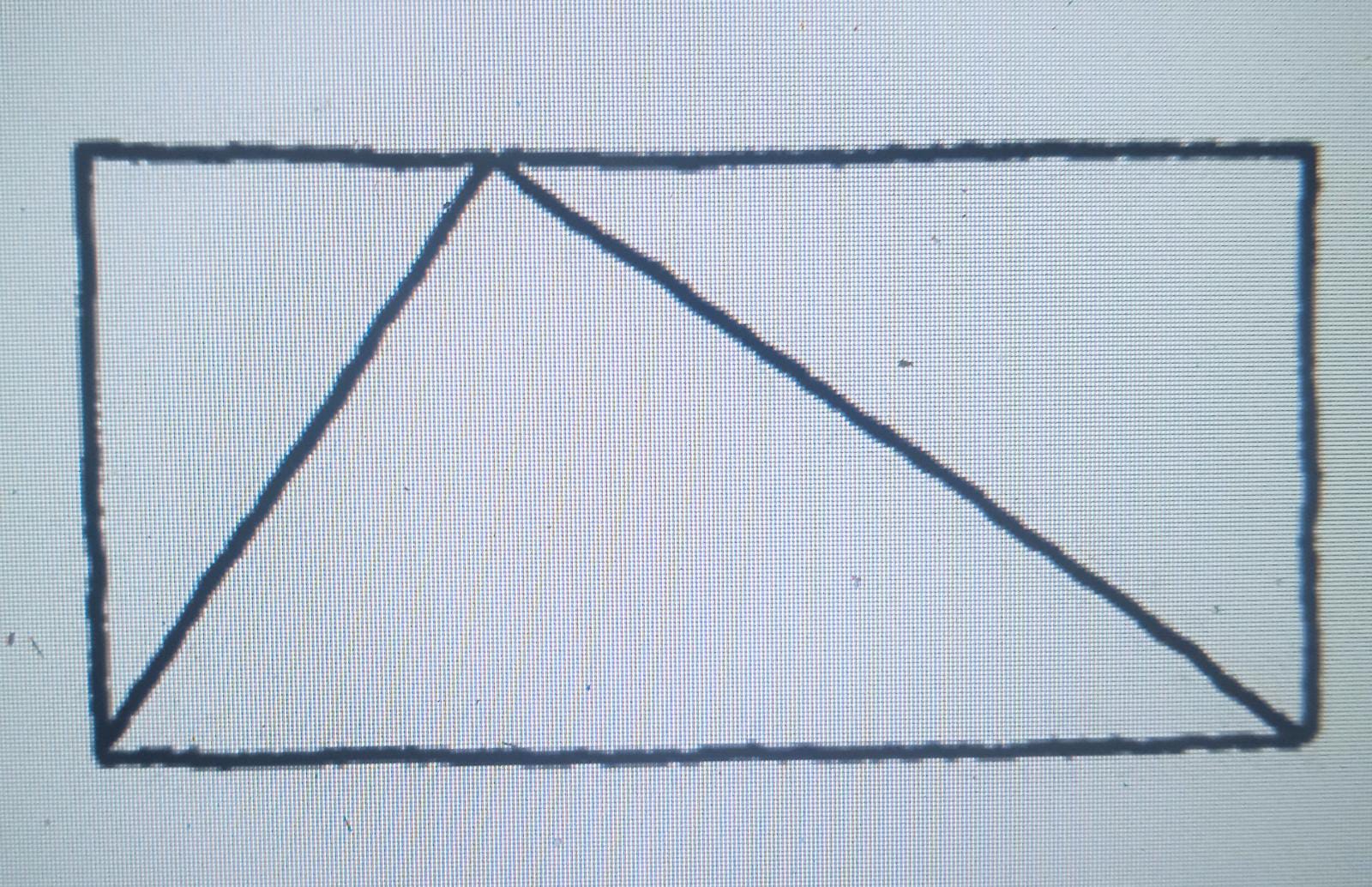
Contenido matemático: la fórmula para el área de un triángulo es base x altura / 2
-
A cargo de Juan y MarcosLectura eje: segunda parte del capítulo 1 del libro de Lockhart (currículo escolar).(Queda adjunto un pdf con algunas cosas extraidas de esa parte.)1) Empezamos haciendo un punteo de las ideas principales de la segunda parte del primer capítulo del libro de Lockhart.En particular, mencionamos- cómo la matemática (o mas precisamente la educación) tiene un formato escalonado, en el que se somete a los estudiantes a nuevas simbologías progresivamente, sin desarrollar intuiciones o generar una experiencia matemática (recordamos la dualidad producto/proceso)- el ejemplo de la geometría, y la sustitución de la intuición geométrica natural por una ofuscación llena de terminologías, notaciónes y postulados muchas veces hasta difíciles de leer2) Hicimos una puesta en común sobre ejemplos de motivaciones o intuiciones que den paso a los conceptos que se trabajan en el liceo.Surgieron:- los complejos para poder desarrollar una "bháskara para polinomios de grado 3" y no meramente como un símbolo que es raíz de
, - la física motivando las derivadas,- los primos como concepto natural a organizar objetos en grupos,- los polinomios de grado dos como expresiones de áreas de rectángulos, definiendo un camino a bháskara,- la naturaleza geométrica e histórica en el Teo. de Pitágoras,- el logaritmo como "contar ceros",- las ecuaciones como modelos a preguntas del mundo natural3) Evaluamos nuestra capacidad de hacer este ejercicio con otras asignaturas, lo que nos hizo ver que en ciertos aspectos este problema no parece propio de la matemática, aunque en Matemática se hace mucho más evidente.4) Cerramos con actividades y acertijos que no son puramente matemáticas, pero son experiencias matemáticas en cuanto nos llevan a profundizar en nuestra capacidad de resolver problemas lógicos, cautivando nuestra curiosidad de esa manera.5) Comentamos la importancia del "momento adecuado" para que se produzca la experiencia, y por lo tanto el aprendizaje significativo. No es cualquier momento, cualquier contexto. A la misma persona hoy puede no interesarle algo que mañana la motiva. También sobre la necesidad de que el estudiante esté en un estado de curiosidad, de apertura.
-
A cargo de Sara Vilar del Valle.
Trabajamos sobre los conceptos de "experiencia óptima" de Mihaly Csikszentmihalyi y de "andamiajes" de Jerome Bruner.
En el estado de "experiencia óptima", la información que lleva a la conciencia es congruente con las metas y la energía psíquica fluye sin esfuerzo (ver foto adjunta).
El andamiaje es un conjunto de estrategias del docente/facilitador, para facilitar la posibilidad de que el aprendizaje suceda (ver foto adjunta).
Adjuntamos materiales que registran cosas de las que conversamos.
Película "La educación prohibida" versión corta:
Película "La educación prohibida" versión completa:
Video "Paradigma del sistema educativo" de Ken Robinson:
-
A cargo de Luciana y Micaela.
Lectura eje: artículo de Thurston (fundamentalmente secciones 4, 5 y 14)
Se conversó sobre la escalera de conocimientos matemáticos, muy alta y muy angosta. Y sobre cómo podría ser positivo ensanchar los pisos de abajo, intentando abarcar la mayor cantidad de temas que tengan la menor cantidad de prerrequisitos. Algunos temas que surgieron en el espíritu de buscar conceptos matemáticos “sin prerrequisitos” fueron los siguientes:
-Concepto de infinito
-Grupos y criptografía, inspirándonos en el cubo de Rubik
-Grafos, caminos y coloraciones
-Temas elementales de medida más allá de integrar
- Problemas de conteo
A partir de esto, apareció la noción de "madurez matemática" y discutimos sobre lo que ello significa. Conversamos sobre la idea de que enfocar en fomentar la madurez matemática del estudiante debería ser, en gran parte, uno de los mayores objetivos de una clase. Además, la madurez matemática de los alumnos podría determinar si un tema resulta entendible para ellos al momento de darlo.
En base a esto surgen las preguntas, ¿hasta qué punto se debería tener en cuenta la madurez matemática de los alumnos al momento de dar una clase? ¿Es posible que un tema específico no tenga prerrequisitos particulares, pero que requiera una determinada “madurez matemática” para ser comprendido? ¿O es justamente el aprender sobre este tema en particular lo que generaría madurez matemática y permitiría al alumno expandir sus horizontes? ¿Dónde uno traza la línea respecto a los temas que podrían verse en el liceo, y los que requieren una madurez matemática mayor?
Compartimos un blog que viene al caso, que presenta temas para tratar en diversas áreas de la matemática, orientado en la mayoría de los casos a gente sin conocimiento previo del tema.
https://infinityplusonemath.wordpress.com/2017/09/23/how-long-is-infinity/, recomendamos ojear las secciónes “Size of infinity”, “Manifold Menagerie” y “Non-measurable Sets That Go Bump in the Night” (esta última es un poco más arriesgada).
Finalmente, con la misma imagen de la escalera, se habló de que cuando el estudiante hace preguntas que se van del camino marcado por la escalera, el docente suele responder que eso no es parte de lo que se va a tratar, esto es, justamente por el piso ser bien angosto, hay poca movilidad hacia los costados. La imagen puede tener que ver con el miedo de caerse, de tambalear. Cuanto más anchos los cimientos, más difícil lastimarse al caer.
-
A cargo de Matías M y Rodri.
Lectura eje: artículo de Thurston (esencialmente sección 4)
Habiendo tratado hasta el momento problemáticas en la educación matemática como tal, nos propusimos abordar la pregunta:¿qué podemos hacer (desde el Centro de Matemática) para ayudar a cambiar la situación actual?Surgieron varias ideas, que punteamos acá abajo:- generar una "base de datos" con contenidos, que pueda ser consultada por docentes en general- presentar proyectos de extensión por ejemplo para trabajar con liceos, escuelas, etc- dictar charlas o talleres puntuales a estudiantes, permitiéndoles tener una experiencia matemática de primera mano, metiéndonos en sus aulas, un día cualquiera, en una de sus clases de matemática, sin hacer demasiado alaraca de que va un matemático- crear un espacio para que los estudiantes de la licenciatura puedan trabajar en charlas/proyectos/etc, ¿tal vez creditizar este tipo de actividad?Las anteriores son a grandes rasgos: medidas a pequeña escala. Se comentó que también podría tomarse una línea más institucional, "política" si se quiere, para producir un cambio.La comunicación entre docentes y matemáticos, especialmente el intercambio entre ellos, es algo que hoy por hoy no se da tanto y que podría resultar sumamente provechoso. Se mencionó al diploma de matemática como vehículo para acercar estas dos puntas.También surgieron otras reflexiones interesantes, no tan relacionadas a la pregunta central.¿Qué hay que llevarse de una clase de matemática? Más que contenidos, habría que focalizarse en la matemática como facilitadora. Enfrentarse a problemas e improvisar sin autocensurarse. Que el que haya cosas verdaderas y falsas no se confunda con que "está mal equivocarse". Intentar, errar y repetir. Habría que enfocarse en aprender a pensar, los contenidos suponen un vehículo para eso. En línea con esto se presentó la cuestión de la corrección como validación, es decir, el hábito del estudiante de no estar convencido de que lo que hizo está bien hasta que "alguna autoridad" así lo diga.
-
Nos visitó Antonio Cafure, de la Universidad Nacional General Sarmiento, Docente Investigador en Matemática que obtuvo previamente un título y experiencia como Profesor de Enseñanza Media y Superior..
Es actualmente docente investigador del Instituto de Desarrollo Humano de la Universidad Nacional de General Sarmiento e Investigador del Conicet. Es además editor de la Revista de Educación Matemática de la Unión Matemática Argentina.
La mayoría de las personas detestan la matemática. En realidad, detestan eso que en la escuela conocieron bajo ese nombre. Habría que interrogarse seriamente sobre si eso que se hace en la primaria y la secundaria tiene alguna relación con lo que la matemática realmente es. Lo que se imparte en las aulas es casi siempre un conjunto de reglas, de arbitrariedades.
La creatividad, la discusión, el espacio para la invención, la posibilidad de hacernos preguntas, todas características esenciales del hacer matemática, brillan por su ausencia. Al menos en Argentina, la ausencia de la matemática en la enseñanza es un síntoma cada vez más manifiesto.
Algunas cosas que nos transmitió Nino:
- el lugar metafórico en la matemática, de no quedarse sólo con lo que sí y lo que no, sino con toda la variedad de narraciones posibles sobre una misma idea, o definición, o demostración, de cómo cada persona puede entender, pensar y relatar la matemática de diferentes maneras, que no todo es tan rígido como parece entenderse a veces, por los propios matemáticos;
- que los propios matemáticos nos cuestionemos qué hacemos mal en nuestro rol docente;
- que dejemos entrar los programas que calculan y la tecnología a las aulas, que nos reciclemos en ese sentido, y aprovechemos del conocimiento de nuestros estudiantes para ayudar.
-
Charla a cargo de Ariel Affonzo
Preguntas sobre el estudiante:
¿Por qué está en esa clase? ¿Para qué está en esa clase?
Respuestas heterogéneas a atender. No dar nada por sentado, cuentos de los monos y de la silla.
Experiencia particular del trabajo en el preu. Rescato de la charla de Ariel la importancia de mantener un nivel de excelencia en las actividades, de desafío a la inteligencia, adaptado a cada estudiante, y al mismo tiempo mantener un nivel de humanidad en los vínculos. Grupo de docentes comprometidos haciendo de ejemplo para grupos de estudiantes comprometidos. Trabajos en equipos con intervención del docente como mero guía, en todas las instancias posibles. No separación de clases teóricas y prácticas.
Ariel mencionó tres referencias hispanoamericanas: Eduardo Sáenz de Cabezón, conocido por su canal de youtube "Derivando", los libros de "Miguel de Guzmán" entre los cuales uno que queda subido a esta página, y también sugirió fuertemente a Claudi Alsina.
-
Charla a cargo de Anthony y Mathias (eje: the importance partial progress en el blog de Terence Tao)
En primera instancia nos centramos en discutir opiniones sobre que entendemos por avance en matemática. En ese aspecto, hubo un consenso general sobre el valor del proceso y no del resultado final. Algunas de las formas que entendemos como avance son por ejemplo equivocarse, transformar el problema o cambiar los puntos de vista.
A partir de lo anterior logramos introducir el concepto de progresión parcial propuesto por Terence Tao que justamente da valor a la parte del proceso. Esto no llevó a cuestionarnos el cómo las evaluaciones tradicionales en general (no solo en matemática) no tienen en cuenta este tipo de avances y como estas tienden a calificar a las personas en vez de evaluarlas.
Se mencionó que los cursos en los cuales las calificaciones no tuvieran tanto peso, lograban ser más satisfactorios, ya que quitan la presión de no aprobar. Así mismo se mencionó que las evaluaciones tradicionales también son una instancia de aprendizaje y que por lo tanto no deberían ser erradicadas por completo. Un ejemplo sería una instancia donde la evaluación sea resolver un único ejercicio y el estudiante pudiera contar todo lo que pensó acerca de él, los caminos que consideró.
Notamos además que las evaluaciones en general se hacen al finalizar un curso, lo que es contraproducente ya que no nos permite cambiar durante el proceso. Además, relacionado con el tema de los recursos observamos que, en nuestro caso, el hecho de ser pocos estudiantes nos permite una evaluación más personal, por ejemplo, la posibilidad de hacer un examen oral permite visualizar mejor el estado de conocimiento de un estudiante y generar una instancia rica de intercambio.
Finalmente retomamos la discusión sobre la progresión parcial, usando de ejemplo este seminario en particular, que reflexiona sobre la enseñanza de la matemática: el hecho de discutir sobre la enseñanza sin aplicarlo directamente ya es en sí mismo un progreso parcial sobre la cuestión. -
Estuvimos conversando con Cecilia, acá abajo enlace a las diapositivas de su charla y enlace a un ejemplo de clase que ella mencionó.
http://bit.ly/seminarioCMAT2022
-
A cargo de Mariana y Santi.
Eje: capítulo "Exhultation" de Lockhart
"In this way, being a mathematician is a lot like being a field biologist. Imagine that you have set up your camp on the outskirts of a tropical jungle, let’s say in Costa Rica. Every morning you take your machete into the jungle and explore and make observations, and every day you fall more in love with the richness and splendor of the place. Suppose you are interested in a particular type of animal, say hamsters. (Let’s not worry about whether there actually are any hamsters in Costa Rica.) The thing about hamsters is they have behavior. They do cool, interesting things: they dig, they mate, they run around and make nests in hollow logs. Maybe you’ve studied a particular group of Costa Rican hamsters enough that you’ve tagged them and given them names. Maybe Rosie is black and white and loves to burrow; maybe Sam is brown and enjoys lying in the sun. The point is that you are watching, noticing, and getting curious. Why do some hamsters behave differently from others? What features are common to all hamsters? Can hamsters be classified and grouped in meaningful and interesting ways? How do new hamsters get created from old ones, and what traits are inherited? In short, you’ve got hamster problems—natural, engaging questions about hamsters that you want answered.Well, I’ve got problems too. Only they are not located in Costa Rica, and they don’t concern hamsters. But the feeling is the same. There’s a jungle full of strange creatures with interesting behaviors, and I want to understand them. For example, among my favorite denizens of the mathematical jungle are these fantastical beasts: 1, 2, 3, 4, 5, . . ."
A partir de este párrafo, introdujimos la idea de "bosque" como una situación que despierta la curiosidad de mirar qué hay dentro. Y entendimos al docente como una especie de "guía turístico" de tal bosque, que lo conoce muy de cerca, que sabe los sitios más peligrosos, los senderos que le resultarán más fáciles a una persona con dificultad en el caminar, los lugares donde hay bichitos más curiosos, etc.
Llevamos el juego "Escondidos" y el juego "Tach" como propuestas "bosques", disparadoras de mirar un poco qué hay ahí dentro. Elegimos esos "bosques" porque eran a priori desconocidos para los participantes y eso podía ayudar a entrar con inocencia y curiosidad, como queremos que entre un estudiante a una propuesta que le hacemos.
-
Charla de Gonzalo Frasca.
Conversamos sobre el asunto de aprender. Apareció la imagen de la muchacha aprendiendo una pirueta sobre su skate. La comparamos con la experiencia de aprender matemática. Nos preguntamos sobre nuestras experiencias de aprender.
Aparece el juego como herramienta fundamental en la instancia de aprendizaje. El videojuego en particular. El feedback inmediato. La autoevaluación inmediata. El aprender para un cierto estatus también.
Gonzalo nos mostró las regletas como herramientas para manejar aritmética en las primeras etapas, y algunos libros de texto diseñados para trabajar con niños de escuelas de Finlandia y Noruega.
Surgieron muchas inquietudes y cuestiones filosóficas en torno a los procesos de aprendizaje y a la tarea de enseñar.
Conversamos sobre las experiencias de escuelas democráticas danesas y sobre la formación de los docentes en los países nórdicos, en particular de las maestras.
Aparecen experiencias de aprendizaje útiles y muy practicables fuera del aula, y eso da espacio a que en el aula sucedan otras cosas.
-