Bioestadística 2022: Ej. 5

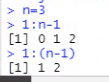
Buenas! Tengo una duda con estas dos lineas. La diferencia es q en la primer linea sin parentesis me arroja tambien el cero pero no entiendo xq ya q le pido de 1 a n-1. Cual seria la utilidad de esta linea sin el parentesis? Gracias

Re: Ej. 5

de VIDAL MATEO - viernes, 9 de septiembre de 2022, 00:17

Tampoco entiendo que pasa con el Ej. 7. para que sirve la linea m% * %m ?
Gracias!!!!!

Re: Ej. 5

de GOICOECHEA VALERIA - viernes, 9 de septiembre de 2022, 08:56

Si te fijas, cuando haces m*m te devuelve un vector (multiplica cada coordenada del primer vector por cada coordenada del seguro vector). Si haces m%*%m, te devuelve un número, es el producto interno de m con m.

Va de nuevo la respuesta:

Supongamos que tenemos el vector

$x= (x_1, \, x_2, \dots, x_n)$ y otro vector

$y= (y_1, y_2, \dots, y_n)$ . Entonces:

Si hago $x$ * $y$ , R me devuelve el vector: $(x_1 y_1, \, x_2 y_2, \dots, x_n y_n)$ (multiplica cada coordenada de $x$ con cada coordenada de $y$ ).
- Si hago $x$ %*% $y$ , R me devuelve el número: $x_1 y_1 + x_2 y_2 + \dots+ x_n y_n$ (multiplica cada coordenada de $x$ con cada coordenada de $y$ y las suma, a eso se la llama el producto interno de $x$ con $y$ y normalmente se lo escribe como $\left\langle x, y \right\rangle$ ).

Es decir, R se guarda estos símbolos de * o %*% para realizar esas operaciones con vectores.

Saludos

Re: Ej. 5

de GOICOECHEA VALERIA - viernes, 9 de septiembre de 2022, 08:47

Si te fijas,

En el primer caso, R entendió que querías hacer:
1:n (que en este caso es el vector (1, 2, 3)) y luego restarle un 1 a cada coordenada, es decir, entendió:
(1,2,3) -1

En el segundo caso, entendió que querías el vector 1:(n-1), es decir, 1:2, por eso te devolvió el (1,2).

La moraleja es que hay que tener cuidado con cómo escribimos (y usar paréntesis).