Mientras cursaba Física Computacional se propusieron  varios temas para desarrollar y presentar en clase que me hicieron interesar en la Física no lineal. En uno de los trabajos intermedios propuestos , una de las opciones era "Solitones" ... lo elegí simplemente porque jamás había escuchado esa palabra. Aprovecho a que tengo algunas de las simulaciones para hablar de ese tema. 

Este es un fenómeno observado por primera vez por John Scott Russell, un arquitecto y constructor de barcos escocés, en uno de los canales de Edimburgo.  El lo decribía así:

"Estaba observando el movimiento de un barco que se movía rápidamente a lo largo de un canal estrecho por un par de caballos, cuando el barco se detuvo repentinamente; no así la masa de agua en el canal que había puesto en movimiento; se acumuló alrededor de la proa del barco en un estado de violenta agitación, luego, dejándola repentinamente atrás, rodó hacia adelante con gran velocidad, tomando la forma de una gran elevación solitaria, un montón de agua redondeado, liso y bien definido, que continuó su curso a lo largo del canal aparentemente sin cambio de forma ni disminución de velocidad. Lo seguí a caballo y lo alcancé rodando todavía a una velocidad de ocho o nueve millas por hora, conservando su figura original, unos treinta pies de largo y de un pie a pie y medio de alto. Su altura disminuyó gradualmente y después de una persecución de una o dos millas lo perdí en las curvas del canal. Tal fue, en el mes de agosto de 1834, mi primera entrevista casual con aquel singular y hermoso fenómeno”

Actualmente la población cercana a ese canal (que ahora lleva el nombre de JSR) se reúne ciertos días del año a esperar los solitones y algunos hasta se animan a surfearlos. 

¿Cuáles son as principales características de estas ondas tan especiales con las que este constructor se obsesionó hasta su muerte?

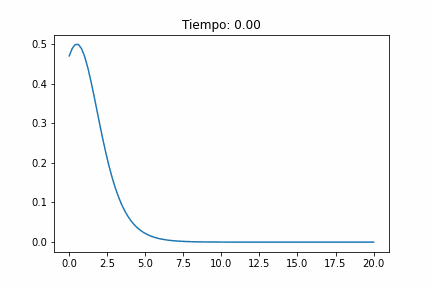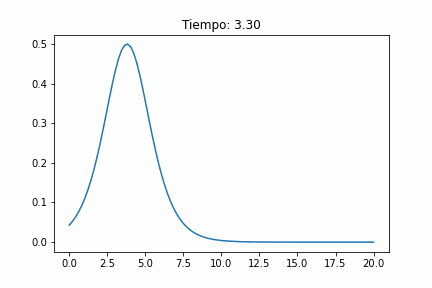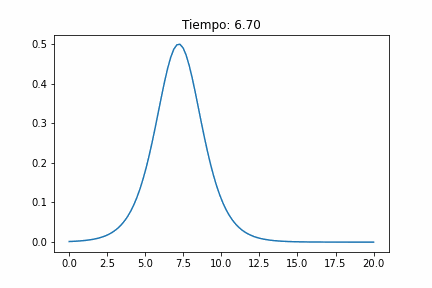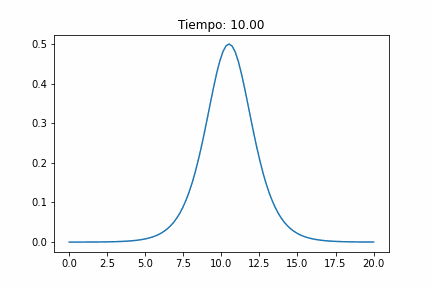
Es una onda localizada en el espacio, con forma  específica, regular y simétrica. La velocidad constante a lo largo de grandes distancias sin cambiar su forma.

Las ondas con mayor amplitud A viajan más rápido que aquellas con amplitudes más pequeñas.  c^2= g(h + A).  No aparece el tiempo!

No se combina con otras olas. Si una se mueve más rápido que otra, puede pasarla sin que ninguna de las dos ondas se deforme por ello.

Se divide en dos olas de diferentes tamaños si es demasiado grande para la profundidad del agua.

Una forma de onda inicial arbitraria puesta en movimiento en el canal evoluciona en dos o más ondas que se mueven a diferentes velocidades y se separan progresivamente hasta formar ondas solitarias individuales.

El ancho  depende de la profundidad del agua.

Si dos solitones tienen el mismo sentido, y uno se mueve más rápido que otro, puede pasarlo sin que ninguna de las dos ondas se deforme por ello.

Se dice que son ondas imposibles de neutralizar.

Pero aunque JSR dedicó el resto de su vida al estudio y registro de este fenómeno, la comunidad científica se mostró dudosa, no podían creer que existieran ondas con esas propiedades. Casi al final de su vida , algunos físicos reconocieron su trabajo: En 1872  Boussinesq intentó explicar las ondas en aguas poco profundas, lo que condujo a una ecuación  que demostró que las ondas solitarias son teóricamente posibles. En 1877 Lord Rayleigh desarrolló de forma independiente teorías similares sobre las ondas y también reconoció a S.R, quien falleció en 1882.

En 1895, Diederik Korteweg y Gustav de Vries ampliaron el trabajo de Boussinesq y desarrollaron una ecuación que demuestra que las ondas solitarias son teóricamente posibles. La ecuación KdV no introduce disipación, lo que significa que puede usarse para describir ondas que viajan largas distancias conservando su forma y velocidad. 

Muchos años después, en 1965, los investigadores Martin Krustal y Norman Zabusky estudiaron la ecuación KdV con más detalle. Descubrieron que las ondas solitarias pueden ocurrir no sólo teóricamente sino también de forma natural, acuñando el término solitones para describirlas. Además, ya no se pensaba en los solitones sólo en el contexto de las ondas del agua, sino que se investigaban aplicaciones en óptica, acústica y otras áreas.

Ecuación Korteweg–de Vries   (KdeV)

SOLITÓN :   Elemento matemático.  Solución a una ecuación diferencial en derivadas parciales dispersiva y  no lineal.  No disipativa.

1. Es una solución localizada de esa ecuación de ondas. LOCALIZADO (razón del sufijo “on” , como una partícula)

2. Forma y velocidad constantes.

3. Se conserva al colisionar con otros solitones.

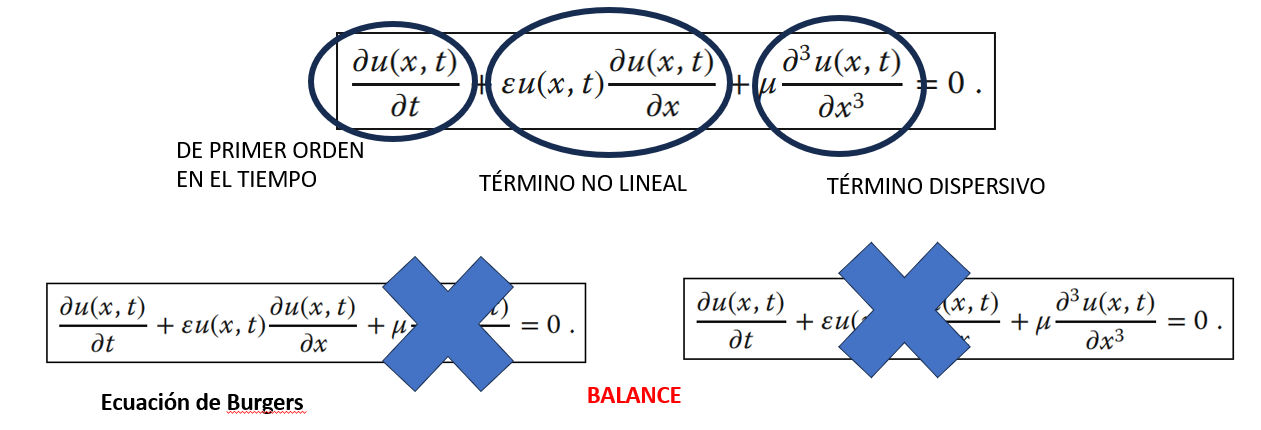
 Vemos primero la ecuación de Burgers

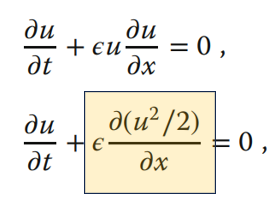
El segundo término, no lineal, provoca que los puntos de la onda se mueven  de tal manera que la velocidad local depende de la amplitud de la onda local, con las partes altas de la onda moviéndose progresivamente más rápido que las partes bajas. Si comenzamos con un paquete de ondas que tiene una variación suave en altura, las partes altas acelerarán y se abrirán paso hacia el frente del paquete, formando así un borde de ataque afilado conocido como onda de choque.

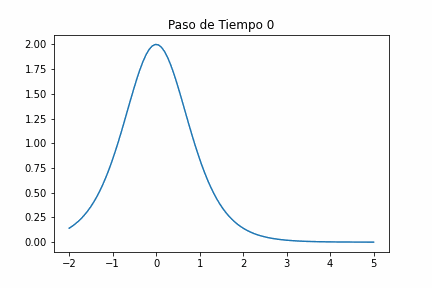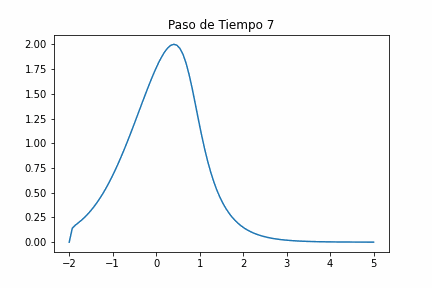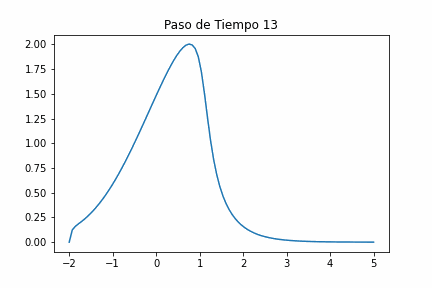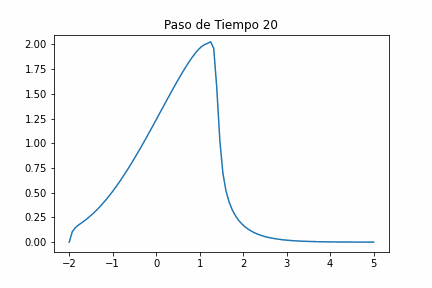
Dispersión

Un fenómeno de onda inversa es la dispersión, en el que una forma de onda se dispersa o se ensancha a medida que viaja a través de un medio. La dispersión no hace que las ondas pierdan energía y se atenúen, sino que pierdan información con el tiempo. Físicamente, la dispersión puede surgir cuando el medio de propagación tiene estructuras con una regularidad espacial igual a alguna fracción de una longitud de onda. Matemáticamente, la dispersión puede surgir de términos de la ecuación de onda que contienen derivadas espaciales de orden superior.

Solución KdeV

Para los parámetros y condiciones iniciales adecuados, el ensanchamiento dispersivo equilibra exactamente el estrechamiento no lineal y se forma una onda viajera estable. La forma es la de un coseno hiperbólico.