Ecuación de varianza estimada

Ecuación de varianza estimada

by TOSAR CAMILA -
Number of replies: 2

Buenas, tengo una duda sobre la ecuación de varainza estimada, ya que aparecen diferentes en el práctico y en el térico grabado. 

En el práctico aparece como la sumatoria por 1/(n-1).


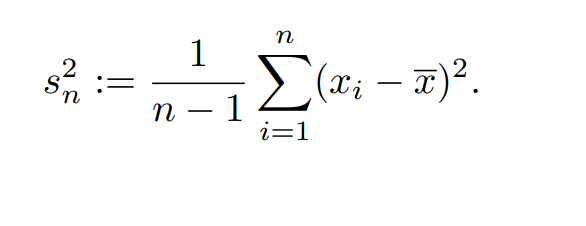
En el térico aparece como la sumatoria por 1/n



In reply to TOSAR CAMILA

Re: Ecuación de varianza estimada

by GOICOECHEA VALERIA -
Hola Camila,

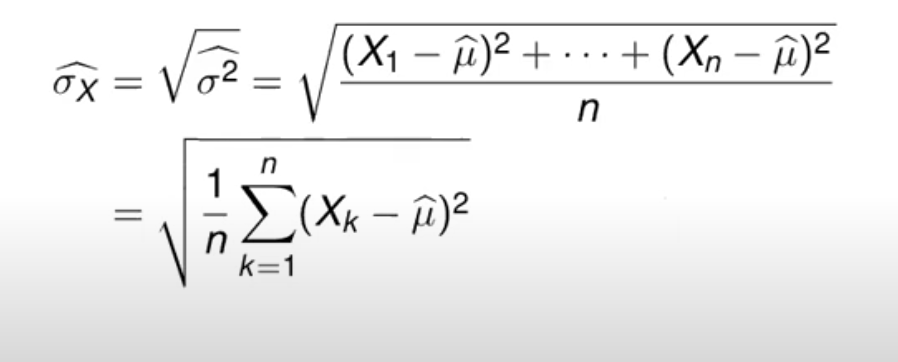
¡Es una excelente pregunta! Los dos son buenos estimadores de  \sigma^2 ya que por la Ley de los Grandes Números:
\sigma_n^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i- \bar{x}_n)^2 \rightarrow \sigma^2
s_n^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i- \bar{x}_n)^2 \rightarrow \sigma^2

(los dos convergen a \sigma^2 ). Sin embargo, la diferencia entre ellos es que la variable aleatoria  s_n^2 verifica que  \mathbb{E}(s_n^2) = \sigma^2 (se dice que es un "estimador insesgado") mientras que  \mathbb{E}(\sigma_n^2) \neq \sigma^2 (no es un estimador insesgado), por eso consideramos que el s_n^2 es mejor como estimador de \sigma^2 .

¿Se entiende?

Saludos