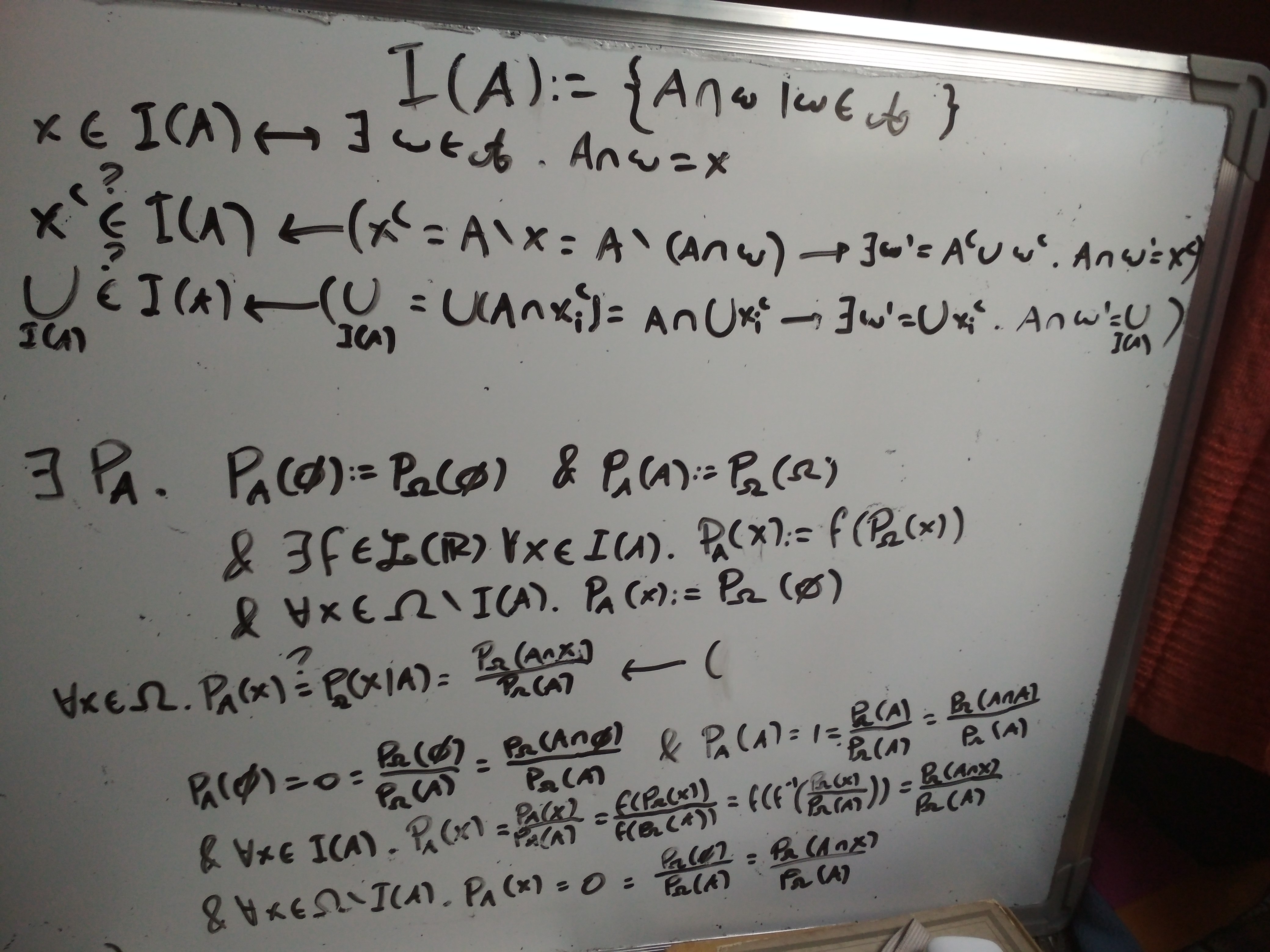Esa es la imagen.
La idea viene de lo último que dijo Juan en la última clase de práctico. Me tomé el tiempo de formalizarlo y me parecía que a alguno le podía interesar.
Como fui bastante denso al escribir, paso a explicar línea por línea a nivel intuitivo. No escribí que el A cursiva (distinto del A imprenta) es una sigma álgebra de algún conjunto Omega. Y que A imprenta, al que voy a llamar sólo A acá, es un subconjunto de Omega.
- Defino I(A). I viene de Intersección. La idea es que me tomo el conjunto que surge de intersectar cada elemento de A cursiva con A.
- Y en este sólo lo reformulo.
- En esta y la siguiente, pruebo que verdaderamente esto es una sigma álgebra. La flecha al revés quiere decir que lo siguiente es una prueba de lo anterior. En este caso pruebo que si un elemento está en I(A), su complemento también.
- En esta pruebo que la unión numerable de elementos que pertenecen también pertenece. Faltaría probar que no es vacío, que es claro tomando omega como el conjunto vacío, con lo que la intersección con A es vacía, y el vacío pertenece.
- Acá paso a definir una probabilidad sobre esta sigma álgebra en función de una probabilidad sobre Omega. Faltó probar que verdaderamente es una probabilidad. Primero lo defino para el vacío (aunque no sea necesario) y para A mismo.
- Y después digo que para cualquier otro elemento en I(A), el valor de la probabilidad está dado linealmente en función de las probabilidades de Omega. Que como fijé un punto en la línea anterior, hay una sóla función posible.
- Y en esta digo que cualquier valoro que no esté en I(A), vale 0 y listo.
- A partir de acá, demuestro que esta definición se corresponde con la de P( . |A). Y lo hago mostrando en cada una de las definiciones de la probabilidad en A, que se corresponden.
- P_A del vacío es 0, y P del vacío dado A también. La correspondencia también se da para P_A(A).
- En este como P_A(A) vale 1, puedo dividir entre él tranquilamente. Después utilizo la tercera definición de P_A, y la propiedad de que f es lineal y llego a lo que quería.
- Por último, por definición de I(A), la intersección entre A y cualquier elemento de A cursiva no me puede dar un elemento que no pertenezca a I(A), por lo que la intersección entre A y cualquier elemento que no pertenece a I(A) es vacía.