Buenas, el ejercicio 6 e plantea que debemos Hallar el valor C que cumple:
i) P{Z ≥ C} = 0.25; ii) P{Z ≤ C} = 0.0287; iii) P{−C ≤ Z ≤ C} = 0.95 .
y no me queda claro si este es un ejercicio que se pueda resolver de forma escrita con la formula hallada en la parte d (1-2K) o si se hace con R.
en caso de que se resuelva con R, que tipo de comando ingreso?
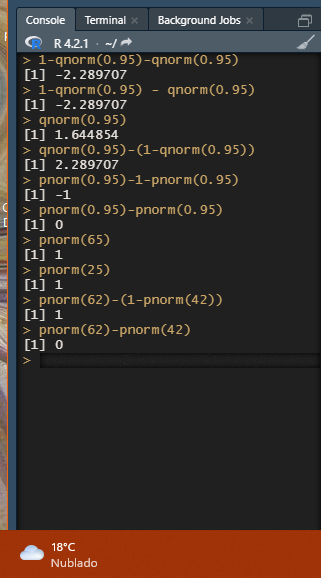
Profes, pude encontrar el comando pero hay algo que estoy haciendo mal y no comprendo. tanto el iii) P{−C ≤ Z ≤ C} = 0.95 como todos los del ejercicio 7a no concuerdan con la solucion.
Me pasó lo mismo, tampoco me quedó claro si debía resolverlo con R o de otra forma, tal vez lo explicaron en clase.
Yo lo hice usando la tabla de distribución normal (está en la web) y me dieron bien los resultados.
Te paso enlace de youtube donde explican como razonarlo. Saludos
Para calcular C, si tengo la probabilidad:
Para calcular C, si el valor de la probabilidad no está en la tabla:
Yo lo hice usando la tabla de distribución normal (está en la web) y me dieron bien los resultados.
Te paso enlace de youtube donde explican como razonarlo. Saludos
Para calcular C, si tengo la probabilidad:
Para calcular C, si el valor de la probabilidad no está en la tabla:
Hola, el comando 
devuelve el valor 
para el cual una normal estándar 
cumple 
. Si en vez de 0 y 1 le pasan otros números, calculan para otras normales.
devuelve el valor para el cual una normal estándar cumple . Si en vez de 0 y 1 le pasan otros números, calculan para otras normales.Por lo tanto:
y obtienen como 
.- Por simetría respecto al eje Y de la campana estándar,
por lo que pueden conseguir 
.
Saludos